Se você clicou neste título, provavelmente está em busca de uma vantagem. Talvez uma planilha de ‘desdobramento inteligente’, uma análise de ‘números quentes’ ou apenas uma confirmação de que a sua intuição está certa.

Eu tenho essa resposta para você. E ela não é baseada em palpites, mas em uma simulação computacional de 1 milhão de jogos que eu rodei pessoalmente.

Adianto que o que os dados mostram é brutal. Mas existe, sim, uma estratégia matematicamente garantida de ganhar dinheiro com loterias. Fique comigo até as últimas linhas deste artigo que eu vou te revelar qual é.

Eu sou Engenheiro de Dados. Minha ferramenta de trabalho não é a sorte (as vezes é sim). Meu negócio é lógica, estatística e processamento de dados em escala. Por isso, decidi colocar a Mega Sena à prova. Peguei todo o histórico de concursos e criei códigos em Python para simular não apenas os próximos jogos, mas milhões de realidades paralelas. O código-fonte completo dessa simulação, incluindo o tratamento dos dados históricos e o motor de simulação, está disponível no meu GitHub para quem quiser auditar ou replicar os experimentos.

O que encontrei nos dados é surpreendente, contra-intuitivo e, talvez, um pouco doloroso para quem vende ‘fórmulas mágicas’. Mas antes de eu te mostrar os gráficos, vamos fazer um teste rápido de intuição?

O Teste de Intuição

Imagine que você precisa escolher um jogo para a Mega da Virada. Qual destas opções você diria que tem a MAIOR chance de ser sorteada? E qual tem a MENOR chance?

• A) A Diagonal: 01 – 12 – 23 – 34 – 45 – 56
• B) Só Ímpares: 03 – 15 – 27 – 33 – 51 – 59
• C) A Sequência: 01 – 02 – 03 – 04 – 05 – 06
• D) Múltiplos de dez: 10 – 20 – 30 – 40 – 50 – 60
• E) “Jogo Bem Distribuído”: 04 – 13 – 28 – 35 – 42 – 58

Segure sua resposta. Vamos aos dados.

1. A Memória das Bolinhas: Existe padrão na Mega Sena?

A primeira coisa que analisamos é a frequência. É comum ouvir: “O número 10 está atrasado (há muito tempo sem ser sorteado), ele tem que sair!”.

Aqui precisamos ser honestos sobre a física da coisa: A Mega Sena não tem memória. As bolinhas não sabem que saíram semana passada. Elas são pedaços de matéria inanimada dentro de um globo giratório.

Ao analisar recortes de jogos reais, o cenário parece ser de caos. Por exemplo, se olharmos apenas os últimos 40 concursos, a frequência estatística esperada seria de 4 aparições por dezena. Mas vemos uma distorção enorme:

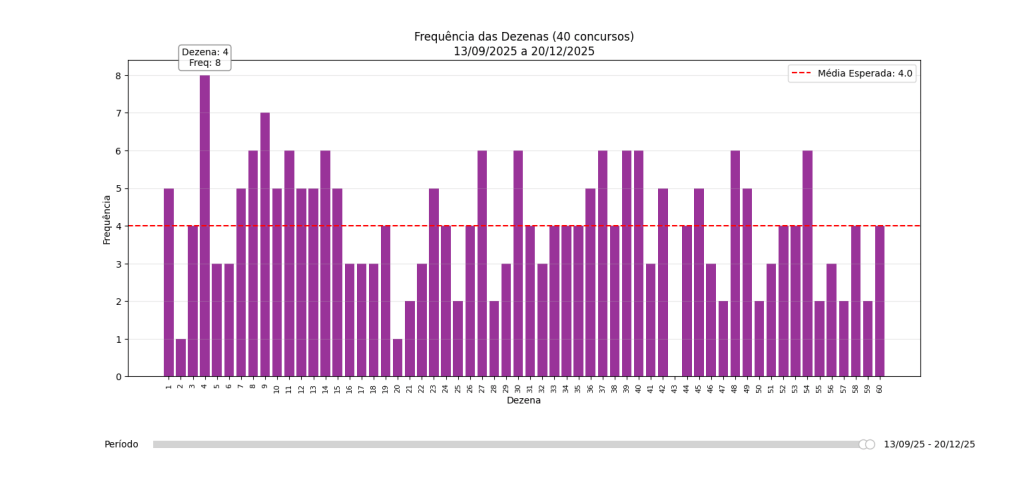
• O número 04 apareceu 8 vezes (o dobro do esperado!);
• Já o número 43 não apareceu nenhuma vez (ele é, inclusive, o mais ‘atrasado’ da base atual. Ele foi sorteado pela última vez em 23/08/2025).

Olhando apenas para isso, a intuição grita que existe um padrão ou um “vício” na urna.

Mas veja o que acontece quando damos um ‘zoom out’ e olhamos para todo o histórico real da Mega Sena (exatos 2.954 concursos até hoje):

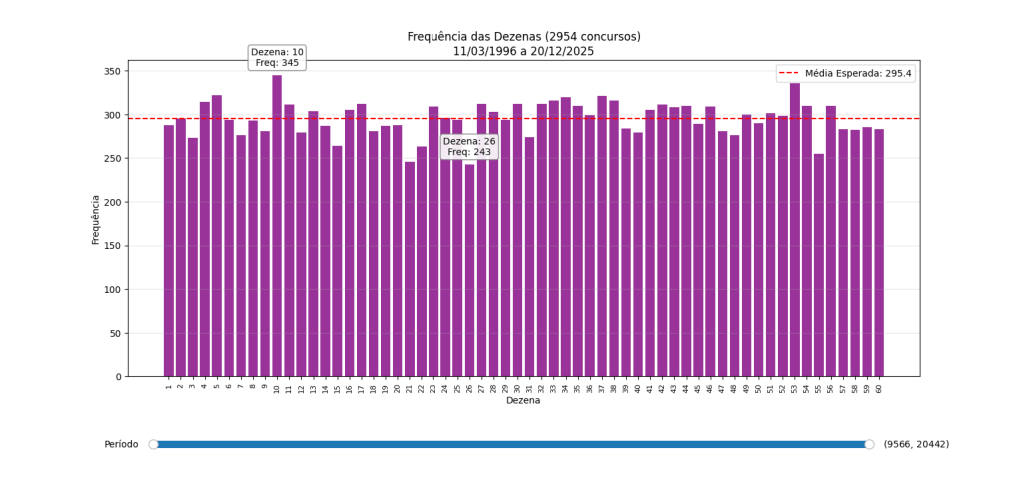
Aquela diferença brutal entre ‘sair o dobro’ e ‘não sair nada’ começa a desaparecer. No histórico completo, o número mais sorteado (o 10) e o menos sorteado (o 26) têm uma diferença de frequência muito menor proporcionalmente do que vimos na amostra curta. A realidade já mostra a tendência de equilíbrio.

Porém, 2.954 jogos ainda é pouco para a matemática ser perfeita. O gráfico real ainda é um pouco ‘dentado’.

Para ver o destino final dessa tendência, rodei minha simulação em Python para 1 milhão de concursos. E aí sim, com tempo suficiente, acontece a mágica da Lei dos Grandes Números.

Na simulação de longo prazo, aquela vantagem do número 10 desaparece completamente. Ele passa a ser sorteado na mesma proporção que o 26.

No gráfico final, a variação desaparece. Todas as barras convergem para a média, ficando levemente acima ou abaixo dela, mas sem nenhum destaque relevante. É a prova visual da equiprobabilidade.

2. A Curva do Sino:A Estatística dos Sorteios

Se a frequência individual não ajuda, que tal a soma? A soma das dezenas de um jogo pode variar de 21 (1+2+3+4+5+6) a 345 (55+56+57+58+59+60). A média teórica fica exatamente no meio: 183.

Ao analisar os dados, vemos que a soma das dezenas segue uma Distribuição Normal, formando o desenho de um sino perfeito.

Mas o que isso significa?A Distribuição Normal (ou Curva de Gauss) é aquele gráfico que é alto no meio e baixo nas pontas. Ela aparece em tudo na natureza: na altura das pessoas, no peso de frutas, e também na loteria.

Isso acontece por causa de uma regra mágica chamada Teorema do Limite Central. Simplificando muito: ele diz que quando somamos os resultados de eventos independentes (como o valor de cada bola sorteada), o total tende a se agrupar na média.

Pense comigo:

• Para a soma dar 21 (o mínimo possível), você precisa tirar EXATAMENTE os números 1, 2, 3, 4, 5 e 6. Só existe uma combinação no universo que dá esse resultado. É raríssimo. Por isso, o gráfico é baixinho na ponta esquerda.
• Para a soma dar 183 (a média), existem milhões de combinações diferentes de números misturados (altos e baixos) que chegam nesse valor. Por isso, o gráfico é alto no meio (o topo do sino).

A maioria dos sorteios vai cair ali no “gordo” do sino, perto da soma 183, simplesmente porque existem mais combinações matemáticas que resultam nessa soma.

“Aha! Então devo jogar números que somam 183!”

Calma. É aqui que mora o perigo. A estatística descreve o comportamento do grupo, não da unidade.

Saber que a maioria dos sorteios cai no meio da curva ajuda a prever o comportamento da loteria ao longo de 100 anos, sendo inclusive (aliada a outros fatores) uma ferramenta poderosa para detecção de fraudes. Mas isso não diz absolutamente nada sobre o próximo sorteio.

Existem milhões de combinações diferentes que resultam na soma 183. Saber as somas mais frequentes não te dá os números. O sorteio não é de uma soma específica, o sorteio é de dezenas independentes.

NOTA TÉCNICA: O “Sino Amassado” da Realidade

Se você plotar apenas os dados reais dos quase 3.000 concursos que ocorreram até hoje, o gráfico não será esse sino perfeito e liso da simulação. Ele parecerá um “sino amassado”, cheio de dentes e irregularidades.

Isso não é uma falha da matemática, é apenas falta de tempo. Para que o Teorema do Limite Central se manifeste visualmente com essa perfeição, 3 mil jogos é uma amostra pequena. Como podemos ver no vídeo, precisaríamos de aproximadamente 20.000 concursos para que o gráfico da vida real atingisse a suavidade visual da curva teórica.

Como esperar por 20.000 sorteios levaria mais de 150 anos, o código serve justamente para “acelerar o tempo”. Ele nos mostra hoje a perfeição estatística que a realidade só revelaria no século XXII.

3. O Experimento da Sala de Aula (A Prova Definitiva)

Se você ainda acha que a sequência 01 – 02 – 03 – 04 – 05 – 06 é impossível, vamos sair do mundo das bolinhas e ir para uma sala de aula.

Imagine uma turma com 60 alunos. A professora precisa formar uma comissão de 6 alunos para organizar a festa de fim de ano. Ela escreve o nome de todos em papéis idênticos, coloca em uma urna e sorteia 6 nomes.

A ordem não importa: se o João for o primeiro ou o último sorteado, ele está no grupo do mesmo jeito.

Agora, visualize dois grupos possíveis:

• Grupo A (Os Primeiros da Lista): A professora sorteia exatamente os nomes dos alunos de nº 01, 02, 03, 04, 05 e 06.
• Grupo B (A Turma do Fundo): A professora sorteia os nomes dos alunos de nº 04, 13, 28, 35, 42 e 58.

Aqui estão as respostas para as perguntas que vão destravar seu cérebro:

1. Quantos grupos diferentes de 6 alunos a professora pode formar?
   Existem exatas 50.063.860 combinações possíveis de grupos. É muita combinação.
2. Qual é o grupo mais provável de ser formado? Nenhum. Não existe um “super grupo” de alunos que a mão da professora prefere pegar.
3. Qual é o grupo menos provável de ser formado? Nenhum. Para a professora (o acaso), pegar os papéis dos alunos 1, 2, 3, 4, 5 e 6 dá exatamente o mesmo trabalho mecânico e probabilístico do que pegar os papéis dos alunos 4, 13, 28, 35, 42 e 58.

O “Click” Mental: A Culpa é das Etiquetas

Você acha o Grupo A estranho porque o seu cérebro adora colocar etiquetas nas coisas. Nós olhamos para os números e colamos rótulos neles: “par”, “ímpar”, “sequência”, “dezena baixa”, “múltiplo de 10”.

• Quando sai 01-02-03-04-05-06, seu cérebro acende o alerta: “Olha! Uma sequência perfeita! Isso é raro!”
• Quando sai 04-13-28-35-42-58, seu cérebro não encontra nenhum rótulo óbvio e diz: “Ah, só números aleatórios. Normal.”

A verdade é que, se trocássemos os números das bolinhas por símbolos abstratos (como ■, ▲, ●, ★, ⬟, ⬢), você não conseguiria distinguir qual grupo é ‘especial’ e qual é ‘comum’.

Lembre-se: qualquer jogo é igualmente raro quando se tem mais de 50 milhões de combinações possíveis. O sorteio é de elementos independentes, e não de números que atendam a critérios estéticos X ou Y.

4. A Resposta do Teste (E o Resultado da Minha Pesquisa)

Apliquei esse teste em grupos reais e o resultado confirmou o viés psicológico: a maioria esmagadora apontou a Opção C (1-6) como “impossível” e a Opção E (Bem Distribuída) como “segura”.

Contudo, como vimos, a probabilidade de TODAS as opções é idêntica (1 em 50.063.860).

Então, existe algum motivo racional para escolher a Opção E?

Sim, mas o motivo não é matemático, é econômico.

• Cenário 1 (A Sequência): Muita gente joga sequências óbvias (1-2-3-4-5-6) ou datas comemorativas. Se esses números forem sorteados, você terá que dividir o prêmio com milhares de outras pessoas. Sua fatia milionária pode virar troco de padaria.
• Cenário 2 (O “Aleatório”): Jogos “feios” ou sem padrão visual (como a Opção E) são menos escolhidos pelo público. Se você ganhar com eles, a chance de dividir o prêmio com menos gente é muito maior.

Resumo: Jogar números “aleatórios” não aumenta sua chance de ganhar, mas protege o valor do seu prêmio na remota hipótese de vitória.

Conclusão

Eu rodei as simulações. Tentei encontrar brechas. Mas a matemática é teimosa.

Se você joga pela emoção, pelo ritual de fim de ano com a família, divirta-se. É um entretenimento válido. Mas se você joga achando que encontrou um padrão que a ciência ignorou, eu tenho um gráfico de Gauss e um script em Python que provam o contrário.

Não existe estratégia, planilha ou mandinga que supere a aleatoriedade de eventos independentes.

Para encerrar, deixo a única verdade absoluta sobre como lucrar consistentemente com jogos de azar:

A única forma garantida de ganhar na loteria é sendo o dono da loteria.

Boa sorte. (Estatisticamente, você vai precisar.)